| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 뉴런 신경망
- 머신러닝 과정
- 회귀 알고리즘 평가
- 더미 기법
- LinearRegression 모델
- 이상치 처리
- 수치형 자료
- 알고리즘 기술
- 웹 크롤링
- 딥러닝 역사
- 스케이링
- 지도학습
- 평가용 데이터
- 지니 불순도
- 데이터 분리
- 분류 머신러닝 모델
- 명목형
- 데이터 전 처리
- 불순도
- 가중치 업데이트
- 다중선형 회귀
- 학습용데이터
- 수치 맵핑 기법
- 경사하강법
- 지도학습 분류
- ICDL 파이썬
- MSEE
- 퍼셉트론
- 결측값 처리
- 항공지연
- Today
- Total
끄적이는 기록일지
[머신러닝] 03.지도학습-회귀_(3) 회귀 성능 지표 본문
[머신러닝] 03.지도학습-회귀_(3) 다중 선형 회귀
[머신러닝] 03.지도학습-회귀_(2) 단순 선형 회귀 [머신러닝] 03.지도학습-회귀_(1) 회귀 아이스크림 가게를 운영한다고 가정하면 지금까지 판 데이터를 가지고 우리는 예상되는 아이스크림 판매량
kcy51156.tistory.com
1. 회귀 알고리즘 평가
1) 어떤 모델이 좋은 모델인지 평가할 때는 목표에 얼마나 잘 달성했는지 정도를 평가한다.
2) 실제 값과 모델이 예측하는 값의 차이에 기반한 평가 방법 사용하는데
ex) RSS, MSE, MAE, MAPE, R²
2. RSS – 단순 오차

1) 실제 값과 예측 값의 단순 오차 제곱 합
2) 값이 작을수록 모델의 성능이 높음
3) 전체 데이터에 대한 실제 값과 예측하는 값의 오차 제곱의 총합

4) RSS 특징
- 가장 간단한 평가 방법으로 직관적인 해석이 가능함
-그러나 오차를 그대로 이용하기 때문에 입력 값의 크기에 의존적임
- 절대적인 값과 비교가 불가능
3. MSE, MAE – 절대적인 크기에 의존한 지표
1) MSE(Mean Squared Error)
- 평균 제곱 오차, RSS 에서 데이터 수 만큼 나눈 값
- 작을수록 모델의 성능이 높다고 평가할 수 있음.

* Loss(모델에서 줄여야할 값) → MSE(회귀) 지표
Entropy(분류)
2) MAE(Mean Absolute Error)
- 평균 절댓값 오차, 실제 값과 예측 값의 오차의 절대값의 평균
- 작을수록 모델의 성능이 높다고 평가할 수 있음.
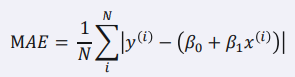
3) MSE, MAE 특징
- MSE: 이상치(Outlier) 즉, 데이터들 중 크게 떨어진 값에 민감함
- MAE: 변동성이 큰 지표와 낮은 지표를 같이 예측할 시 유용
- 가장 간단한 평가 방법들로 직관적인 해석이 가능함
- 그러나 평균을 그대로 이용하기 때문에 입력 값의 크기에 의존적임

- 절대적인 값과 비교가 불가능함
4) 𝑹² (결정 계수)
- 회귀 모델의 설명력을 표현하는 지표
- 1에 가까울수록 높은 성능의 모델이라고 해석할 수 있음

* RSS값이 작을수록 1에 가까워져 좋은 성능의 모델이 되고,
TSS보다 크다면 음수가 되어 성능이 나쁜 모델이 된다.
- 𝑻𝑺𝑺는 데이터 평균 값과 실제 값차이의 제곱
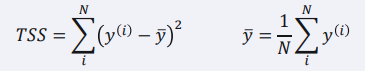
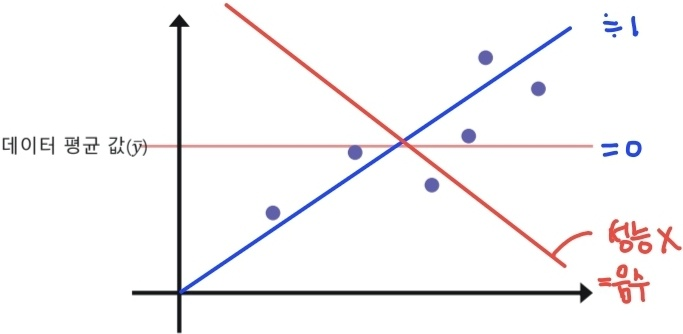
- 오차가 없을수록 1에 가까운 값을 가짐
- 값이 0인 경우, 데이터의 평균 값을 출력하는 직선 모델을 의미함
- 음수 값이 나온 경우, 평균값 예측 보다 성능이 좋지 않음.
4. 실습
Sales 예측 모델의 성능을 평가하기 위해서 다양한 회귀 알고리즘 평가 지표를 사용하여 비교해보겠습니다.
1. train_X 데이터에 대한 MSE, MAE 값을 계산하여 MSE_train, MAE_train에 저장합니다.
2. test_X 데이터에 대한 MSE, MAE 값을 계산하여 MSE_test, MAE_test에 저장합니다.
# 회귀 알고리즘 평가 지표 - MSE, MAE
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
# 데이터를 읽고 전 처리합니다
df = pd.read_csv("Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
# 다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
# train_X 의 예측값을 계산합니다
pred_train = lrmodel.predict(train_X)
"""
1. train_X 의 MSE, MAE 값을 계산합니다
* mean_squared_error(y_true, y_pred): MSE 값 계산하기
* mean_absolute_error(y_true, y_pred): MAE 값 계산하기
"""
MSE_train = mean_squared_error(train_Y, pred_train)
MAE_train = mean_absolute_error(train_Y, pred_train)
print('MSE_train : %f' % MSE_train)
print('MAE_train : %f' % MAE_train)
# test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
"""
2. test_X 의 MSE, MAE 값을 계산합니다
"""
MSE_test = mean_squared_error(test_Y, pred_test)
MAE_test = mean_absolute_error(test_Y, pred_test)
print('MSE_test : %f' % MSE_test)
print('MAE_test : %f' % MAE_test)
>>> MSE_train : 2.705129
MAE_train : 1.198468
MSE_test : 3.174097
MAE_test : 1.460757학습 경우가 테스트 경우보다 좀 더 높았고 MSE가 MAE보다 큰값을 가지는 걸 볼 수 있다.
3. train_X 데이터에 대한 R2 값을 계산하여 R2_train에 저장합니다.
4. test_X 데이터에 대한 R2 값을 계산하여 R2_test에 저장합니다.
# 회귀 알고리즘 평가 지표 - R2
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
# 데이터를 읽고 전 처리합니다
df = pd.read_csv("Advertising.csv")
df = df.drop(columns=['Unnamed: 0'])
X = df.drop(columns=['Sales'])
Y = df['Sales']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, test_size=0.2, random_state=42)
# 다중 선형 회귀 모델을 초기화 하고 학습합니다
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
# train_X 의 예측값을 계산합니다
pred_train = lrmodel.predict(train_X)
"""
3. train_X 의 R2 값을 계산합니다
"""
R2_train = r2_score(train_Y, pred_train)
print('R2_train : %f' % R2_train)
# test_X 의 예측값을 계산합니다
pred_test = lrmodel.predict(test_X)
"""
4. test_X 의 R2 값을 계산합니다
"""
R2_test = r2_score(test_Y, pred_test)
print('R2_test : %f' % R2_test)
>>> R2_train : 0.895701
R2_test : 0.899438테스트가 좀 더 높긴 하지만 대체로 비슷한 값이 나온다는 걸 볼 수 있다.
'AI실무' 카테고리의 다른 글
| [머신러닝] 04.지도학습-분류_(2) 의사결정나무-불순도 (1) | 2021.10.03 |
|---|---|
| [머신러닝] 04.지도학습-분류_(1) 분류란 (1) | 2021.10.03 |
| [머신러닝] 03.지도학습-회귀_(3) 다중 선형 회귀 (0) | 2021.09.25 |
| [머신러닝] 03.지도학습-회귀_(2) 단순 선형 회귀 (0) | 2021.09.25 |
| [머신러닝] 03.지도학습-회귀_(1) 회귀 (0) | 2021.09.25 |




