| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 데이터 전 처리
- 결측값 처리
- 데이터 분리
- 스케이링
- 수치형 자료
- 머신러닝 과정
- MSEE
- 더미 기법
- 수치 맵핑 기법
- 명목형
- 지니 불순도
- 학습용데이터
- 항공지연
- 지도학습 분류
- 딥러닝 역사
- 뉴런 신경망
- 분류 머신러닝 모델
- 회귀 알고리즘 평가
- 평가용 데이터
- 지도학습
- 다중선형 회귀
- 이상치 처리
- LinearRegression 모델
- 가중치 업데이트
- 경사하강법
- 알고리즘 기술
- ICDL 파이썬
- 웹 크롤링
- 불순도
- 퍼셉트론
- Today
- Total
끄적이는 기록일지
[머신러닝] 03.지도학습-회귀_(2) 단순 선형 회귀 본문
[머신러닝] 03.지도학습-회귀_(1) 회귀
아이스크림 가게를 운영한다고 가정하면 지금까지 판 데이터를 가지고 우리는 예상되는 아이스크림 판매량만 주문하길 원한다. 이 때 평균 기온을 활용하여 판매량을 예측할 수 있다면? 1. 문제
kcy51156.tistory.com
지난 시간에 이에 단순 선형 회귀에 대해 알아보겠습니다.
1. 단순 선형 회귀
1) 데이터를 설명하는 모델을 직선 형태로 가정
2) 𝑌 ≈ 𝛽0 + 𝛽1𝑋 가정
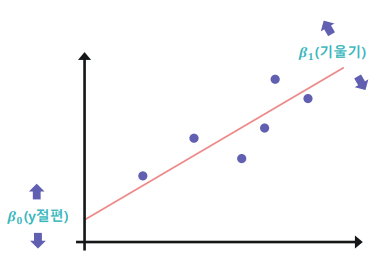
직선을 구성하는 𝜷𝟎(y절편)와 𝜷𝟏(기울기)를 구해야함.
3) 실제 정답과 내가 예측한 값과의 차이가 작을수록 좋음

- 실제 값과 예측 값의 차이를 구하기.

- 실제 값과 예측 값의 차이의 합으로 비교하기에는 예외가 존재한다.
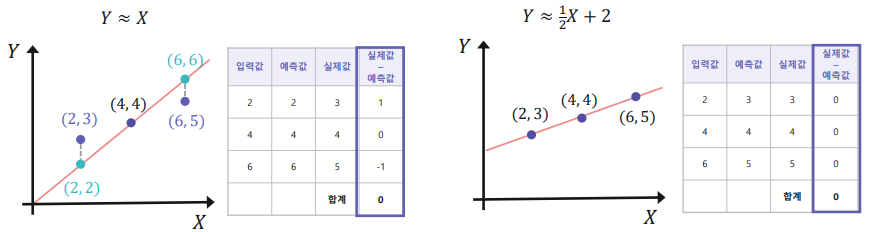
- 실제값-예측값이 일치하지 않았는데 총 합계가 0이 나오는 경우가 존재한다. → 그렇기에 차이의 제곱의 합으로 비교

2. Loss함수
1) 실제 값과 예측 값 차이의 제곱의 합 (작을수록 좋은 모델)
Y ≈ 𝛽0 + 𝛽1X

* 1/n은 평균 구하기 위해
- i 번째 데이터 (𝑥 𝑖(입력값) , 𝑦 𝑖(실제값)) 에 대해:
예측 값: 𝛽0𝑥 𝑖 + 𝛽1
2) Loss 함수에서 주어진 값은 입력 값과 실제 값이다.
- 𝜷𝟎(y절편), 𝜷𝟏(기울기) 값을 조절하여 Loss 함수의 크기를 작게 한다.
3) Loss 함수 줄이기
- Loss 함수의 크기를 작게 하는 𝜷𝟎(y절편), 𝜷𝟏(기울기)를 찾는 방법 → 경사하강법(Gradient descent)

3. 경사하강법
- 계산 한 번으로 𝜷𝟎 , 𝜷𝟏 을 구하는 것이 아니라 초기값에서 점진적으로 구하는 방식
- 𝜷𝟎, 𝜷𝟏 값을 Loss 함수 값이 작아지게 계속 업데이트 하는 방법
1) 𝜷𝟎, 𝜷𝟏 값을 랜덤하게 초기화
2) 현재 𝜷𝟎, 𝜷𝟏 값으로 Loss 값 계산
3) 현재 𝜷𝟎, 𝜷𝟏 값을 어떻게 변화해야 Loss 값을 줄일 수 있는지 알 수 있는 Gradient 값 계산
4) Gradient 값을 활용하여 𝜷𝟎, 𝜷𝟏 값 업데이트
5) Loss 값의 차이가 거의 없어질 때까지 2~4번 과정을 반복
(Loss 값과 차이가 줄어들면 Gradient 값도 작아짐)

4. 단순 선형 회귀
1) 단순 선형 회귀 과정을 정리해보면,
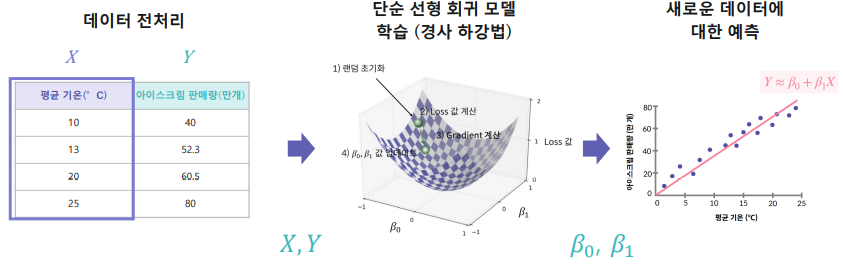
2) 단순 선형 회귀 특징
- 가장 기초적이나 여전히 많이 사용되는 알고리즘
- 입력값이 1개인 경우에만 적용이 가능함
- 입력값과 결괏값의 관계를 알아보는 데 용이함
- 입력값이 결괏값에 얼마나 영향을 미치는지 알 수 있음
- 두 변수 간의 관계를 직관적으로 해석하고자 하는 경우 활용
5. 실습
1. X 데이터를 column 명이 X인 DataFrame으로 변환하고 train_X에 저장합니다.
2. 리스트 Y를 Series 형식으로 변환하여 train_Y에 저장합니다.
3. sklearn의 LinearRegression() 모델을 lrmodel에 초기화 합니다.
4. fit을 사용하여 train_X, train_Y 데이터를 학습합니다.
5. lrmodel을 학습하고 train_X의 예측값을 구하여 pred_X에 저장합니다.
import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# scikit-learn사용하면 Loss 함수를 최솟값으로 만드는 β10, β1 을 쉽게 구할 수 있다.
from sklearn.linear_model import LinearRegression
#주어진 데이터 -> 사용하기 위해선 선형 모델(LinearRegression)에 적용하려면 전 처리 필요
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
# LinearRegression 모델의 입력값으로는 Pandas의 DataFrame의
# feature (X) 데이터와 Series 형태의 label (Y) 데이터를 입력 받을 수 있습니다.
#(X, Y의 샘플의 개수는 같아야함)
"""
1. X의 형태를 변환하여 train_X에 저장합니다.
"""
train_X = pd.DataFrame(X, columns=['X'])
"""
2. Y의 형태를 변환하여 train_Y에 저장합니다.
"""
train_Y = pd.Series(Y)
# 변환된 데이터를 출력합니다.
print('1. 전 처리한 X 데이터: \n {}'.format(train_X))
print('전 처리한 X 데이터 shape: {}\n'.format(train_X.shape))
print('2. 전 처리한 Y 데이터: \n {}'.format(train_Y))
print('전 처리한 Y 데이터 shape: \n\n{}'.format(train_Y.shape))
# 모델 학습
"""
3. 모델을 초기화 합니다.
* sklearn의 LinearRegression() 모델을 사용하려면 우선 해당 모델 객체를 불러와 초기화해야합니다.
"""
lrmodel = LinearRegression()
"""
4. fit을 사용하여 학습에 필요한 train_X, train_Y 데이터를 학습합니다.
"""
lrmodel.fit(train_X, train_Y)
# 학습한 결과를 시각화하는 코드입니다.
plt.scatter(X, Y) #X,Y데이터를 점으로 출력
# plot 선 긋는 함수 c='r' 빨강색
plt.plot([0, 10], [lrmodel.intercept_, 10 * lrmodel.coef_[0] + lrmodel.intercept_], c='r')
# 범위
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.title('Training Result')
plt.savefig("test.png")
"""
5. train_X에 대해서 예측합니다.
* predict 함수 : DataFrame 또는 numpy array인 X 데이터에 대한 예측값을 리스트로 출력한다.
"""
pred_X = lrmodel.predict(train_X)
print('5. train_X에 대한 예측값 : \n{}\n'.format(pred_X))
print('실제값 : \n{}'.format(train_Y))
>>> 1. 전 처리한 X 데이터:
X
0 8.701538
1 3.908258
2 1.893624
3 3.287300
4 7.393330
5 2.989846
6 2.257572
7 9.844507
8 9.945895
9 5.483216
전 처리한 X 데이터 shape: (10, 1)
2. 전 처리한 Y 데이터:
0 5.644131
1 3.758766
2 3.872333
3 4.409904
4 6.438450
5 4.028278
6 2.261060
7 7.157690
8 6.290974
9 5.196929
dtype: float64
전 처리한 Y 데이터 shape: (10,)
5. train_X에 대한 예측값 :
[6.2546398 4.18978504 3.32191889 3.92228833 5.6910886 3.79415077
3.47870087 6.74700964 6.7906856 4.86824749]
실제값 :
0 5.644131
1 3.758766
2 3.872333
3 4.409904
4 6.438450
5 4.028278
6 2.261060
7 7.157690
8 6.290974
9 5.196929
dtype: float64

'AI실무' 카테고리의 다른 글
| [머신러닝] 03.지도학습-회귀_(3) 회귀 성능 지표 (0) | 2021.09.25 |
|---|---|
| [머신러닝] 03.지도학습-회귀_(3) 다중 선형 회귀 (0) | 2021.09.25 |
| [머신러닝] 03.지도학습-회귀_(1) 회귀 (0) | 2021.09.25 |
| [머신러닝] 02.데이터 전처리_(4) 데이터 정제 및 분리 (1) | 2021.09.15 |
| [머신러닝] 02.데이터 전처리_(3) 수치형 자료 (0) | 2021.09.14 |




