1. 딥러닝의 원리

0. 딥러닝이란

 

딥러닝의 구조 - 집값 모델

1. 집값 모델

1) Supervised Learning(지도학습) : 학습셋이 주어짐

2) 학습셋 : x = [면적], y = 집값

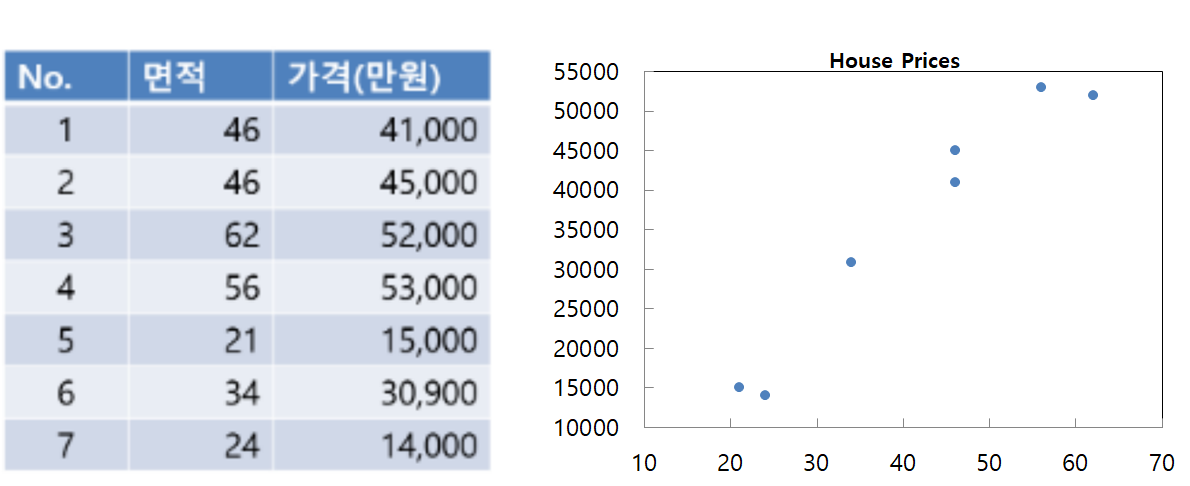
2. 모델 만드는 법?

- 무작정 대입해보기

• 1차 시도: θ0 = 3, θ₁= 5 → 틀림

• 2차 시도: θ0 = 6, θ₁= 100 → 틀림

  

• 3차 시도: θ0 = 60, θ₁= 1000 → 얼추 비슷해짐

  

• 4차 시도 : θ0 = 30, θ₁= 800 → 비슷해짐

  

  4차시도까지 한 결과 점들과 많이 가까워진 것을 확인할 수 있습니다. 하지만 이렇게 임의의 숫자를 대입하는 것을 50번하던 1000번을 하던 우리는 이 값이 더 좋은 식인지 결정할 수 없습니다.이를 해결하기 위해 딥러닝이 나오게 되었습니다.

3. 딥러닝 구조 - 언제 계산을 멈출 수 있나요?

• 무한한 h(x)중 무엇이 좋은 함수인가?
• 찾는다면 어떻게 찾을 수 있는가?

나쁨/틀림을 정의하고 cost/Loss function을 통한

h(x)의 예측 y'와 주어진 학습셋의 y의 차이를 최소화하는 것이 목적(오차가 0에 가까워질 때)

4. 딥러닝 구조 - 비용함수

J(θ) - cost function

계속하면 더 좋아질 수 있지 않을까 생각하기 때문에 여전히 언제 끝날지 알 수 없습니다. 이를 해결해줄 수 있는 경사하강법에 대해 알아보겠습니다.